线形回归
位置:chapter_linear-networks/linear-regression-concise.html
当我们想预测一个数值时,就会涉及到回归问题。常见的例子包括:预测价格(房屋、股票等)、预测住院时间(针对住院病人等)、 预测需求(零售销量等)。但不是所有的预测都是回归问题。
为了解释线性回归,我们举一个实际的例子: 我们希望根据房屋的面积(平方英尺)和房龄(年)来估算房屋价格(美元)。 为了开发一个能预测房价的模型,我们需要收集一个真实的数据集。 这个数据集包括了房屋的销售价格、面积和房龄。 在机器学习的术语中,该数据集称为训练数据集(training data set) 或训练集(training set)。 每行数据(比如一次房屋交易相对应的数据)称为样本(sample), 也可以称为数据点(data point)或数据样本(data instance)。 我们把试图预测的目标(比如预测房屋价格)称为标签(label)或目标(target)。 预测所依据的自变量(面积和房龄)称为特征(feature)或协变量(covariate)。
线形模型:price(价格)=w1(权重)x area(面积)+w2(权重)x age(年龄)+ b(偏置)
给定训练数据特征和对应的已知标签,线性回归的目标是找到一组权重向量和偏置。在开始寻找最好的模型参数(model parameters)w和b之前,还需要两个东西:(1)损失函数:一种模型质量的度量方式;(2)优化算法:一种能够更新模型以提高模型预测质量的方法。
大致流程:准备数据->定义模型->初始化模型参数->定义损失函数->定义优化算法->模型训练->模型预测
随机梯度下降(gradient descent)
它通过不断地在损失函数递减的方向上更新参数来降低误差。
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值) 关于模型参数的导数(在这里也可以称为梯度)。 但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。 因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本, 这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
正态分布与平方损失
正态分布(Normal Distribution)是一种常见的概率分布,通常在自然和社会科学中出现。它的形状呈现出一个“钟型”曲线,因此也被称为“钟形分布”。正态分布有两个重要的参数:
- 均值(μ):分布的中心位置,表示数据的平均值。
- 标准差(σ):反映数据的离散程度,标准差越大,分布越宽,越分散;反之,标准差越小,分布越窄,越集中。
通俗理解钟形曲线:想象一座山,这座山的最高点就是均值(μ),而山的倾斜程度则由标准差(σ)决定。高峰处的概率最高,远离中央位置的概率逐渐降低。
什么叫做服从正态分布?答:一个随机变量如果其概率分布符合正态分布的特征,则称该随机变量“服从正态分布”。这意味着在多次独立实验中,样本数据的分布会逐渐接近一个钟形曲线(正态分布曲线)。
神经网络
神经网络的层数为1。 我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络。对于线性回归,每个输入都与每个输出相连,我们将这种变换称为全连接层(fully-connected layer)或称为稠密层(dense layer)。
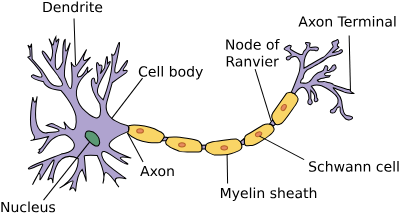
生物学
这是一张由树突(dendrites,输入终端)、 细胞核(nucleus,CPU)组成的生物神经元图片。 轴突(axon,输出线)和轴突端子(axon terminal,输出端子) 通过突触(synapse)与其他神经元连接。
线形回归的实现
不使用深度学习框架(建议先看一遍,在使用深度学习框架):chapter_linear-networks/linear-regression-scratch.ipynb
使用深度学习框架:
from torch import nn
import torch
from d2l.torch import load_array
from d2l import torch as d2l
# 生成数据样本(X)和标签(Y)
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
print('features:', features[0], '\nlabel:', labels[0])
# 读取数据集
batch_size = 10
data_iter = load_array((features, labels), batch_size)
print(next(iter(data_iter)))
# 定义模型
# 第一个指定输入特征形状,即2,第二个指定输出特征形状,输出特征形状为单个标量,因此为1。
net = nn.Sequential(nn.Linear(2, 1))
# 初始化模型参数
# 指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样, 偏置参数将初始化为零
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# 在初始化参数之后,我们的任务是更新这些参数,直到这些参数足够拟合我们的数据。 每次更新都需要计算损失函数关于模型参数的梯度。 有了这个梯度,我们就可以向减小损失的方向更新每个参数。
# 定义损失函数
loss = nn.MSELoss() # 均方误差
# 定义优化算法(不断地在损失函数递减的方向上更新参数来降低误差)
# 其中lr是超参数(可以调整但不在训练过程中更新的参数)
trainer = torch.optim.SGD(net.parameters(), lr=0.03) # 小批量随机梯度下降算法
# 训练
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
# 调用net(X)生成预测并计算损失l(前向传播)
l = loss(net(X), y)
trainer.zero_grad()
l.backward() # 进行反向传播来计算梯度
trainer.step() # 调用优化器来更新模型参数
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
# 进行预测
new_features = torch.tensor([[1.0, 2.0], [3.0, 4.0]]) # 示例特征
predictions = net(new_features)
print('Predictions:', predictions)